INTEGRAL III

INTEGRAL III

Kamis, 04 Desember 2014

INTEGRAL TRIGONOMETRI

 

Pada pembahasan ini kita akan berlatih untuk menyelesaikan integral-integral yang memiliki bentuk

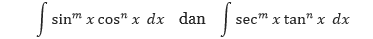
di mana m dan n adalah bilangan bulat positif. Untuk menemukan antiturunan dari bentuk-bentuk tersebut, pecahlah bentuk tersebut menjadi kombinasi dari integral trigonometri sedemikian sehingga kita dapat menggunakan Aturan Perpangkatan.
Sebagai contoh, kita dapat menyelesaikan integral berikut dengan memisalkan u = sin x. Sehingga, du = cos x dx dan diperoleh,

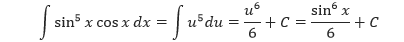
Untuk menyelesaikan integral-integral trigonometri, gunakan identitas-identitas berikut agar kita dapat menggunakan Aturan Perpangkatan.

---

Panduan untuk Menyelesaikan Integral yang Memuat Perpangkatan Sinus dan Cosinus

1. Jika pangkat dari sinus adalah bilangan ganjil dan positif, simpan satu faktor sinus tersebut dan ubahlah faktor sisanya menjadi cosinus. Kemudian, ekspansi dan integralkan.
   
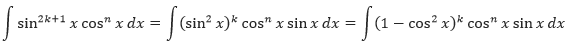
2. Jika pangkat dari cosinus adalah bilangan ganjil dan positif, simpan satu faktor cosinus tersebut dan ubahlah faktor sisanya menjadi sinus. Kemudian, ekspansi dan integralkan.
   
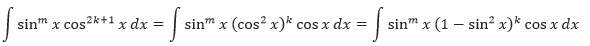
3. Jika pangkat dari sinus dan cosinus keduanya genap dan tidak negatif, gunakan secara berulang identitas berikut,
   
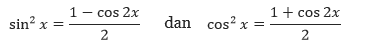
   untuk mengubah integran menjadi perpangkatan ganjil dari cosinus. Kemudian lanjutkan sesuai panduan nomor 2.

---

Contoh 1: Pangkat dari Sinus Ganjil dan Positif
Tentukan,

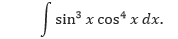
Pembahasan Karena kita berharap untuk menggunakan Aturan Perpangkatan dengan u = cos x, maka simpan satu faktor sinus untuk membentuk du dan ubah faktor-faktor sinus sisanya menjadi cosinus.

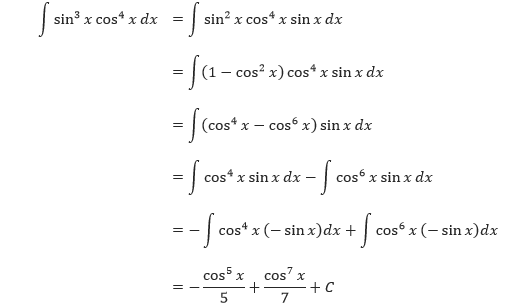
Pada Contoh 1 di atas, pangkat m dan n keduanya merupakan bilangan bulat positif. Bagaimanapun, teknik yang sama dapat digunakan selama salah satu dari m atau n merupakan bilangan ganjil dan positif. Sebagai contoh, pada contoh selanjutnya pangkat dari cosinusnya 3, sedangkan pangkat dari sinusnya –1/2.
Contoh 2: Pangkat dari Cosinus Ganjil dan Positif
Tentukan,

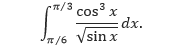
Pembahasan Karena kita akan menggunakan Aturan Perpangkatan dengan u = sin x, maka simpan satu faktor cosinus untuk membentuk du dan ubah faktor-faktor cosinus sisanya menjadi sinus.

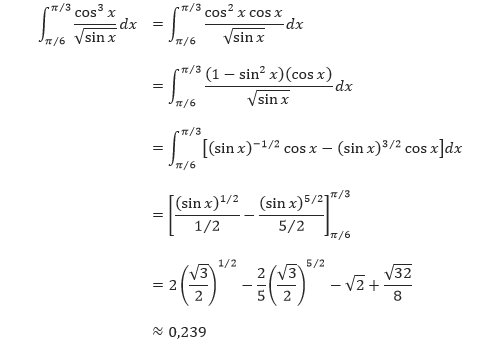
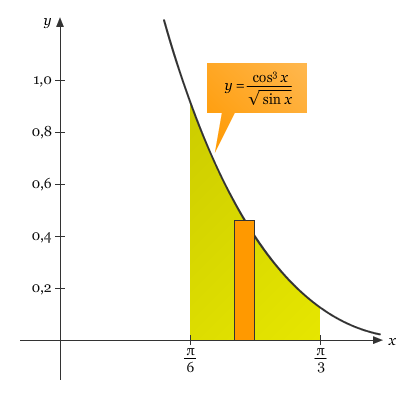
Gambar di bawah ini menunjukkan daerah yang luasnya direpresentasikan oleh integral tersebut.