INTEGRAL I

INTEGRAL I

Kamis, 04 Desember 2014

TEKNIK INTEGRAL: SUBSTITUSI TRIGONOMETRI

 

Ada dua hal yang akan kita diskusikan dalam pembahasan ini. Pertama, kita akan mendiskusikan bagaimana penggunaan substitusi trigonometri dalam menyelesaikan permasalahan integral. Kedua, kita akan juga membahas penggunaan integral dalam memodelkan dan menyelesaikan permasalahan dalam kehidupan sehari-hari.

#174073951 / gettyimages.com

 Substitusi trigonometri dapat digunakan untuk menyelesaikan integral yang memuat bentuk akar

Tujuan dari penggunaan substitusi trigonometri adalah untuk menghilangkan akar tersebut dalam integran. Kita dapat melakukan hal ini dengan menggunakan identitas Pythagoras

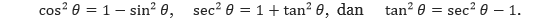
Sebagai contoh, jika a > 0, misalkan u = a sin θ, dengan –π/2 < θ < π/2. Maka

Perhatikan bahwa cos θ ≥ 0, karena –π/2 < θ < π/2.
Substitusi Trigonometri

1. Untuk integral yang memuat √(a² – u²), misalkan u = a sin θ. Maka, didapatkan √(a² – u²) =a cos θ, di mana –π/2 < θ < π/2.
   
2. Untuk integral yang memuat √(a² + u²), misalkan u = a tan θ.
   Maka, √(a² + u²) = a sec θ, dengan –π/2 < θ < π/2.
   
3. Untuk integral yang memuat √(u² – a²), misalkan u = a sec θ. Maka,
   
   

Catatan Batasan dari θ memastikan bahwa fungsi pada substitusi tersebut merupakan fungsi satu-satu. Faktanya, batasan tersebut merupakan interval yang sama di mana arcsinus, arctangen, dan arcsecan didefinisikan.